En informática, el código de Hamming es un código detector y corrector de errores que lleva el nombre de su inventor, Richard Hamming. En los datos codificados en Hamming se pueden detectar errores en uno o en dos bits, y también corregir errores en un solo bit. Esto representa una mejora respecto a los códigos con bit de paridad, que pueden detectar errores en sólo un bit, pero no pueden corregirlo.
Si se añaden junto al mensaje más bits detectores-correctores de error y si esos bits se pueden ordenar de modo que diferentes bits de error producen diferentes resultados, entonces los bits erróneos podrían ser identificados. En un conjunto de siete bits, hay sólo siete posibles errores de bit, por lo que con tres bits de control de error se podría especificar además de que ocurrió un error, qué bit fue el que lo causó.
Hamming estudió los esquemas de codificación existentes, incluido el de dos entre cinco, y generalizó sus conclusiones. Para empezar, desarrolló una nomenclatura para describir el sistema, incluyendo el número de los bits de datos y el de los bits detectores-correctores de error en un bloque. Por ejemplo, la paridad incluye un solo bit para cualquier palabra de datos, así que las palabras del Código ASCII que son de siete bits, Hamming las describía como un código (8.7), esto es, un total de 8 bits de los cuales 7 son datos. En el ejemplo anterior de la repetición, sería un código (3.1), siguiendo la misma lógica. La relación de la información es el segundo número dividido por el primero, por nuestro ejemplo de la repetición, 1/3.
Hamming también estudió los problemas que surgían al cambiar dos o más bits a la vez y describió esto como "distancia" (ahora llamada distancia de Hamming en su honor). La paridad tiene una distancia de 2, dado que cualquier error en dos bits no será detectado. La repetición (3.1)tiene una distancia de 3, pues son necesarios el cambio simultáneo de tres bits para obtener otra palabra de código. La repetición (4.1) (cada bit se repite cuatro veces) tiene una distancia de 4, así que el cambio de dos bits en el mismo grupo quedará sin definir.
Hamming estaba interesado en solucionar simultáneamente dos problemas: aumentar la distancia tanto como sea posible, a la vez que se aumentan al máximo los bits de información. Durante los años 40 desarrolló varios esquemas de codificación que mejoraban notablemente los códigos existentes. La clave de todos sus sistemas era intercalar entre los bits de datos los de paridad.
Hamming (7,4)
Hoy, el código de Hamming se refiere al (7.4) que Hamming introdujo en 1950. El código de Hamming agrega tres bits adicionales de comprobación por cada cuatro bits de datos del mensaje.
El algoritmo de Hamming (7.4) puede corregir cualquier error de un solo bit, y detecta todos los errores de dos bits.
Para un ambiente en el que el ruido pueda cambiar como máximo 2 bits de 7, el código Hamming (7.4) es generalmente el de pérdida mínima.
El medio tendría que ser muy ruidoso para que se perdieran más de 2 bits de cada 7 (casi el 45% de los bits transmitidos), y habría que considerar seriamente cambiar a un medio de transmisión más fiable.
El algoritmo es simple:
1. Todos los bits cuya posición es potencia de dos se utilizan como bits de paridad (posiciones 1, 2, 4, 8, 16, 32, 64, etc.).
2. Los bits del resto de posiciones son utilizados como bits de datos (posiciones 3, 5, 6, 7, 9, 10, 11, 12, 13, 14, 15, 17, etc.).
3. Cada bit de paridad se obtiene calculando la paridad de alguno de los bits de datos. La posición del bit de paridad determina la secuencia de los bits que alternativamente comprueba y salta, a partir de éste, tal y como se explica a continuación.
· Posición 1: comprueba 1, salta 1, comprueba 1, etc.
· Posición 2: comprueba 1, salta 2, comprueba 2, salta 2, comprueba 2, etc.
· Posición 4: comprueba 3, salta 4, comprueba 4, salta 4, comprueba 4, etc.
· Posición 8: comprueba 7, salta 8, comprueba 8, salta 8, comprueba 8, etc.
· Posición 16: comprueba 15, salta 16, comprueba 16, salta 16, comprueba 16, etc.
· Y así sucesivamente.
En otras palabras, el bit de paridad de la posición 2^k comprueba los bits en las posiciones que tengan al bit k en su representación binaria. Dicho a la inversa, el bit 13, por ejemplo, es chequeado por los bits 8, 4 y 1, al ser estos los de su representación binaria: 13=1101(2); 8=1000(2); 4=0100(2); 1=0001(2).
Así pues en la Posición 1, comprobaríamos los bits: 3, 5, 7, 9, 11...; en la Posición 2, los bits: 3, 6, 7, 10, 11, 14, 15...-; en la Posición 4 tendríamos: 5, 6, 7, 12, 13, 14, 15... Así hasta completar la nueva cadena.
Ejemplo
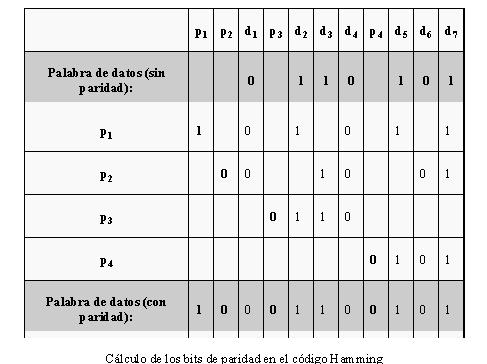
Consideremos la palabra de datos de 7 bits "0110101". Para ver cómo se generan y utilizan los códigos Hamming para detectar un error, observe las tablas siguientes. Se utiliza la d para indicar los bits de datos y la p para los de paridad.
En primer lugar los bits de datos se insertan en las posiciones apropiadas y los bits de paridad calculados en cada caso usando la paridad par.
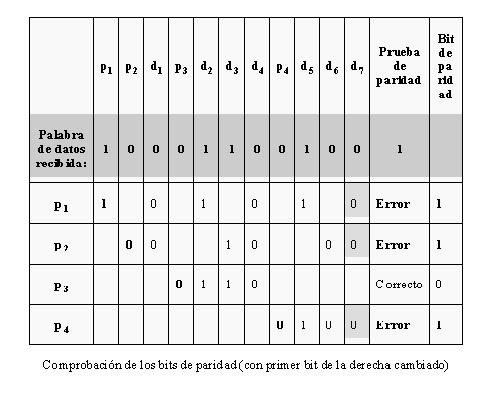
La nueva palabra de datos (con los bits de paridad) es ahora "10001100101". Consideremos ahora que el bit de la derecha, por error, cambia de 1 a 0. La nueva palabra de datos será ahora "10001100100"; cuando se analice el modo en que se obtienen los bits de paridad en los códigos de Hamming se observarán variaciones en la paridad, lo que significará que hay error.
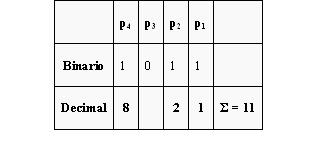
El paso final es evaluar los bits de paridad (recuerde que el fallo se encuentra en d7). El valor entero que representan los bits de paridad es 11, lo que significa que el bit décimo primero de la palabra de datos (bits de paridad incluidos) es el erróneo y necesita ser cambiado.
Cambiando el bit décimo primero 10001100100 se obtiene de nuevo 10001100101. Eliminando los bits de paridad de Hamming se vuelve a obtener la palabra de datos original 0110101.
Observe que en la comprobación de la paridad no se tienen en cuenta los bits de paridad. Si el error se produjera en uno de ellos, en la comprobación sólo se detectaría un error, justo el correspondiente al bit de paridad causante del mismo.
Finalmente, cuando cambien dos bits, en la comprobación de paridad se obtendrá un valor decimal superior a 11, detectándose el error; sin embargo no se podrá saber las posiciones de los dos bits que cambiaron.
REGRESAR A LA PAGINA PRINCIPAL